My answer: Fuck this just give me a rifle and point me towards the enemy lines!
Source

Could you have posted a more badass book cover? Lol
sheeeeiit
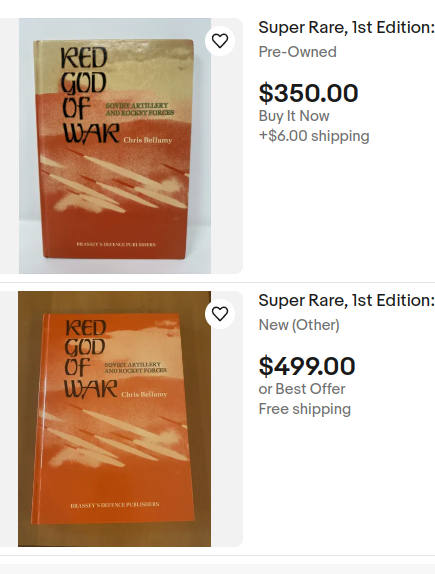
welcome to my hobby. collecting and saving out of print communist literature in a hopes of digitizing them and making them immortal on the internet.
I like to think that out of all the ways I could emulate Stalin, this one’s the best way to honor his memory.
Do you have a rig for book digitizing? I always had an itch to build one when I was in school but I never did
No, I find books and have them sent to my crew to be digitized then archived into our internal library. I know a few other folks in my crew also do similar things with all sorts of media, ranging from old americanized soviet films on those old fashioned film reels to childrens books and magazines to old music composed by the more esoteric parts of communist history.
I think some of the most recent stuff I was a part of in NY was helping one of my crew’s digitizing tech specialists in sorting through old Jewish communist literature and pamphlets, Misha magazines, and old communist vinyl record disks and tape cassettes that CPUSA threw away during their liquidation.
very cool! I am thinking about getting a cnc plywood cutter and designing a flat packable ocr rig would be fun
Just looking up images of a cnc plywood cutter gives my inner creator nerd warm fuzzies just looking at the neat shit you can make with it
Furniture, guillotines, all kinds of neat stuff
you gonna send these over to gen lib or something? a little interested in this one
No but I can DM you access to it
deleted by creator

be nice to that thing, I can’t find it for less than that ebay screenshot
this is really not bad at all for math grow up ppl

not even any funny symbols
You have to understand many of us here are unfortunately American.
oh fuck this, just give me a submachine gun. Only math I need is figuring out how much is left in my mag
yes
I haven’t done this type of math in almost 10 years but yes, I’ll git gud in time
This is a nice little brain teaser. I can’t dedicate time to properly formatting my solutions right now, so I will have to do that later.
Oh, and I missed that there are 5 problems and not 4, so I will need to deal with that one, as well, but it should be easy enough, if my surface skimming of the text is not betraying me.
Damn. I completely forgot about this.
However, none of the problems is hard.
In problem 1, there are some terms that feel like they should cancel out, but they don’t. I even went so far so as to do a sanity check using Wolfram.
In problem 2, the only tricky part is noticing that 0.008^(2*log_c(x)-1) is 0.2^(6*log_c(x)-3).
Problem 3 seems trivial, considering that log_c(x^0) = 0 if we are working with real logarithms, and 27 = 3^3.
Problem 4 just asks for your knowledge of the fact that tg2(x/2) = (1-cos2(x))/(1+cos2(x)). After you use the relevant identity, all you have left is to solve a rather simple equation with respect to cos(x).
Problem 5 - you need to basically just find the length of the lateral side of the trapezium. The angles of the trapezium by the larger base have the angular measure of (2*alpha+(Pi-2*alpha)/2)/2 = alpha/2+Pi/4, because of how angles on a circle depend on corresponding arcs. After that, finding the remaining angles is easy. From there, we can easily find the height of the trapezium, and from there we can find the area of the trapezium and the lateral side of it. From there, we multiply the length of the lateral side of the trapezium by tg(alpha) and get the height of the prism. After that, we multiply the area of the trapezium by the height of the prism and voila.
My official position would likely be ‘cannon fodder’
I can move a box, but very slowly
aims rifle “SOLVE THE PARTIAL DIFFERENTIAL EQUATIONS!”
But I was told I’d be working in the coal mines after the revolution???
I dig holes.
Solve the inequality
Yeah, that’s what we’re trying to do.
i’m about to start fucking barking. i love maths and the idea that my one (1) skill would actually be useful in the USSR instead of just making me prime hiring material for banks is just

Trying out the problems to see how my Indian education(Kerala state govt college education) helps me:
-
In the denominator there is a common a on both sides and can be cancelled. In the right hand side there’s a common c which can be simplified.
And the numerator on the left can be multiplied by 2/2
We can write 4a2(b+c)2n as (2a(b+c)n)2
Then using x2 - y2 = (x - y) (x + y) we can simplify the numerator. -
3 > ln(x)
Edit: ln(x) is bounded on both sides here. Thanking u/ AernaLingus for pointing that out
The complete answer would be 1/2 < ln(x) < 3
Thanking them again.
-
x = e^(-3 ln(3)/(30 - ln(3)^)
-
What’s tg?
Is it tangent? Assumed that and got x = cos-1(1/3) = 1.23095
Well we found our first officer of the artillery corps, everyone.
And the numerator on the left can be multiplied by 2/2
I don’t understand this step. Why did you multiply is for 2/2, I don’t see how it simplifies the numerator on the left, when expanding the fraction sum leads to 4a(b+c)^2n-1, something simpler to factor using x2-y2=(x+y) (x-y)
(2a2 (b+c)2n - 1/2) x 2/2 = (4a2 (b+c)2n - 1) x 1/2
Let’s keep the 1/2 aside for now.We can write 4a2 (b+c)2n as 22 a2 ((b+c)n )2 and 1 as 12
So (4a2 (b+c)2n - 1) = ( 2a(b+c)n )2 - 12
Comparing with x2 - y2 we have x = 2a(b+c)n and y = 1
With with x2 - y2 =(x+y) (x-y), we get:(2a(b+c)n)2 - 12 = (2a(b+c)n + 1) (2a(b+c)n - 1)
We can then cancel the common (2a(b+c)n - 1) term from the numerators on both sides…
with the assumption that 2a(b+c)n - 1 ≠ 0. If it’s zero, then we introduce the issue of 0 x something = 0 x something.
0 x 1 = 0 x 2 = 0
We can’t cancel the common zero and say that 1 = 2. So 0/0 or 1/0 is an issue, but with the assumption that it isn’t 0, we can cancel it out.I multiplied and dividing by 2 because in effect it changes nothing to the result as 2/2 = 1. But it helps to rearrange and simplify stuff.
Ah gotcha. Now it’s all clear.
Could you give me a hand with (2) and (3)? You don’t need to work the whole thing out, but a nudge in the right direction would be greatly appreciated. I feel like I mostly have the knowledge to solve these but I’m just forgetting some crucial rule or I’m just too rusty with my algebra (it’s been a loooong time since I had to do this stuff).
Here’s my work for (2):
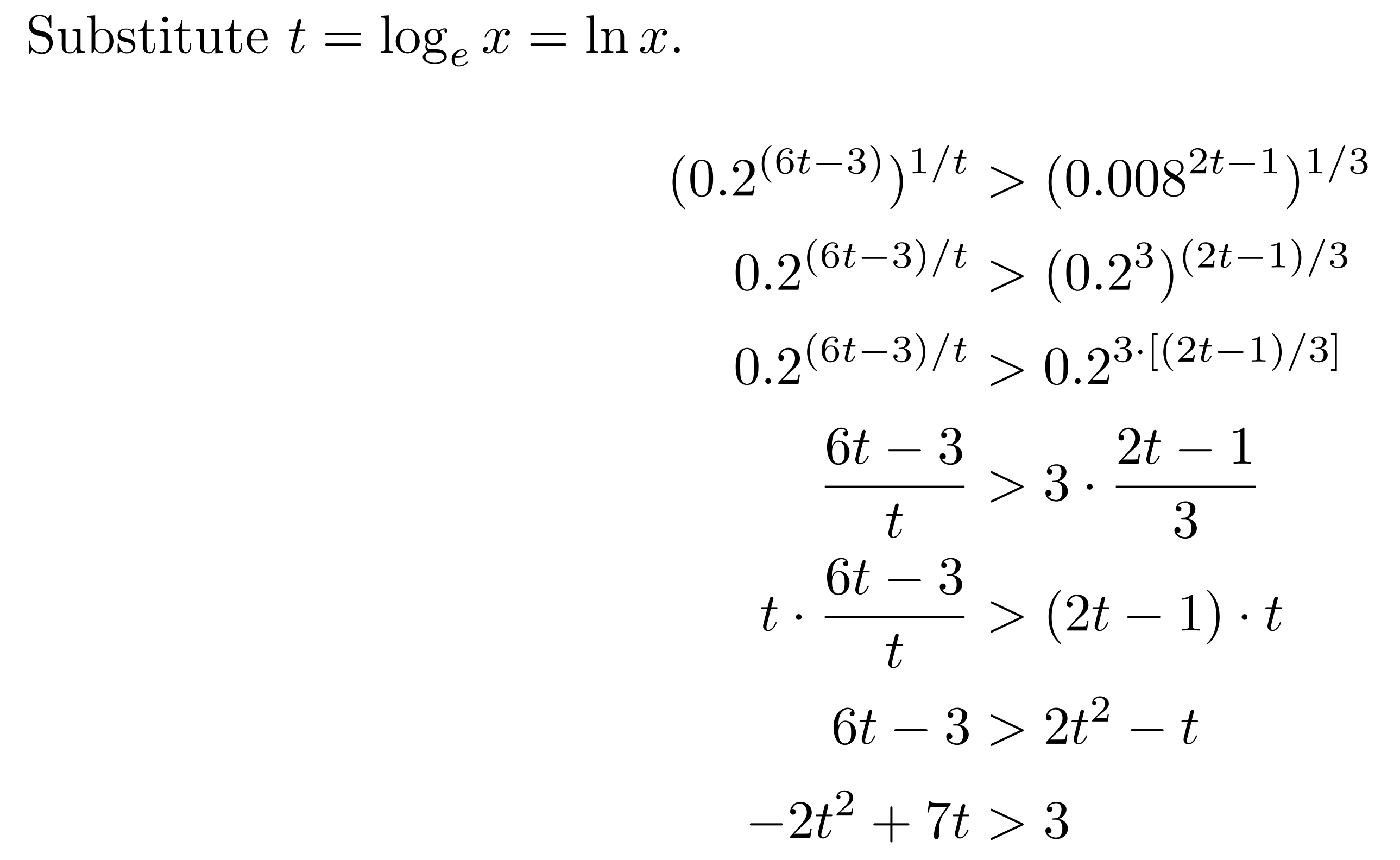
The one part I feel confident about is changing the bases to match so I can just work with the exponents, but the rest feels off.
Here’s my work for (3):
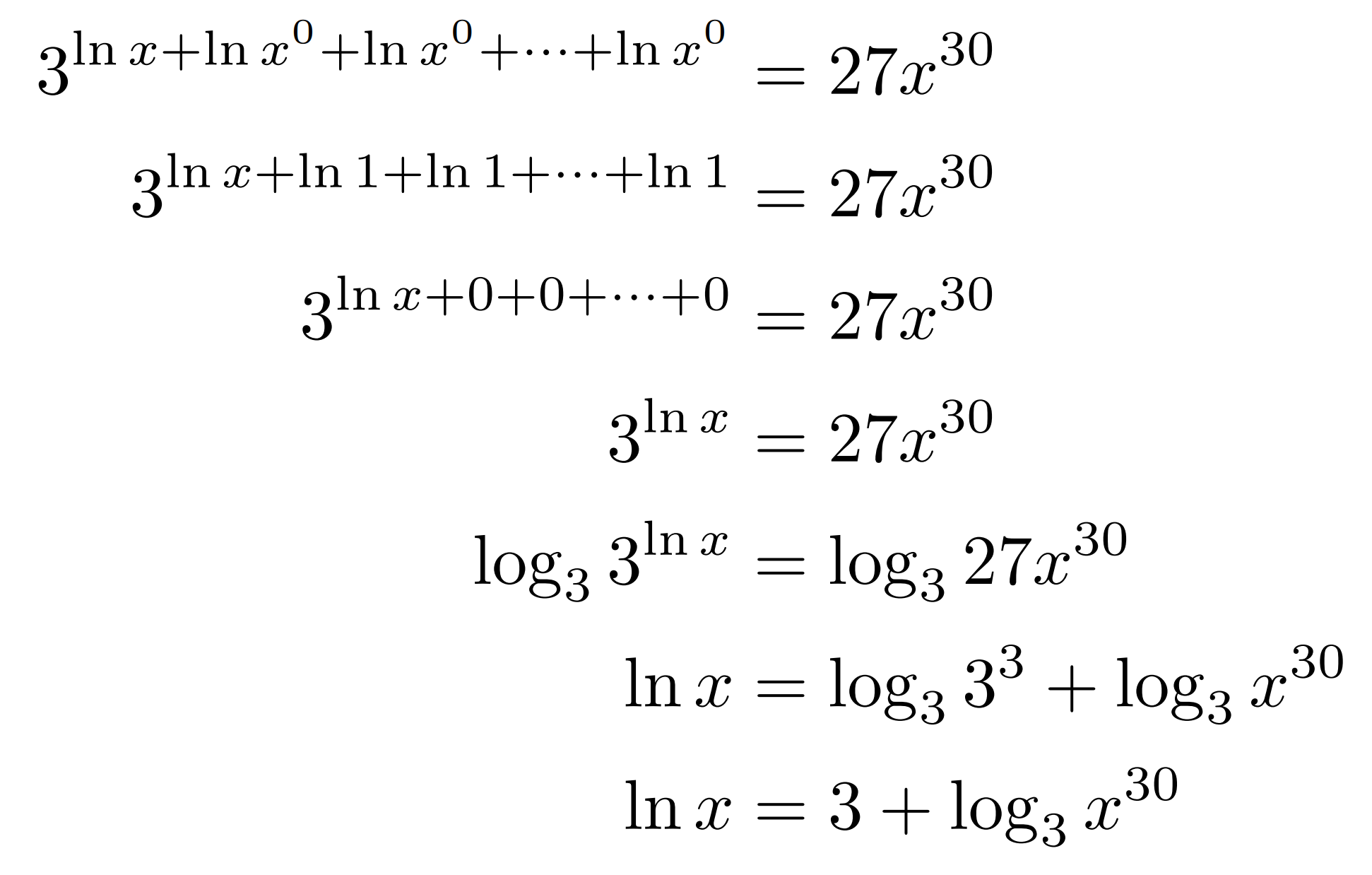
Again, the only part I feel confident about is the silly thing with ln(x0), but I think I went down the wrong path after that based on your answer. I could raise e to both sides to free the x on the left-hand side, but then I’m trapping the x on the right. I guess with both of them I’m struggling with the same thing: what to do when you have a mismatch between one side having a plain variable and the other having a variable inside a logarithm.
As the other comrade said, you’ve got the answers.
For (2)
- 2t2 + 7t -3 > 0
Or 2t2 - 7t -3 <0
We can find the roots and get 2t2 - 7t -3 as (t - 3) (2t - 1) < 0From this we can see that it’s less than zero when t < 3, because the (t - 3) term becomes negative But if t < 1/2, both terms become negative and the equality is not valid.
Thank you. This shows both bounds. I had overlooked that and cancelled the (2t - 1) in a previous step.
So the answer would be 1/2 < ln x < 3
Thanks againFor (3) we have log3 x30 = 30 ln x / ln 3
Using the property loga X = logb X / logb aA question: How did you type of out the equations? LaTeX?
Is there any simple/foss app for it on Android?Thank you! They both seem so simple now that I’ve seen your explanation, but that’s always how it is with these things; I’m sure we’ve all had the experience of nodding along to something in class only to be completely flummoxed by the same material when doing the homework later that day.
With (2), I had a feeling that I needed to factor, but I’ve never been that great at factoring quadratics when the second degree’s coefficient isn’t 1, and even if I had succeeded in factoring I don’t think I would have remembered the logic to work through to get the final inequality. But now I understand thanks to your explanation!
solution for (2)

With (3), for some silly reason I thought that the rule with logaxb = b ⋅ loga x only applied when x = a (no idea why—obviously in that case you just have logaab = b) …as I said, it’s been a while since I did this stuff regularly. That was the key I needed to finish that one!
solution for (3)

Yup, I used LaTeX! I’m not personally familiar with an app targeted at Android, but I used the web-based Overleaf, which is FOSS (AGPLv3). While the website I linked to does require the creation of a free account (which was all I ever needed for my simple undergraduate homework purposes–I think the premium features are only relevant for large projects/teams), you can even self-host it if you’re into that sort of thing.
Incidentally, here’s the LaTeX markup for the problems I worked (nothing fancy, just using the basic math packages with the main feature being the
\alignenvironment which allows me to center the equations around the = or >/< symbols).LaTeX markup
\documentclass{article} \usepackage{amsmath, amsthm, amssymb, amsfonts, mathtools} % ------------------------------------------------------------------------------ \begin{document} % (2) Substitute \(t = \log_{e}{x} = \ln{x}\). \begin{align*} (0.2^{(6t - 3)})^{1/t} &> (0.008^{2t - 1})^{1/3} \\ 0.2^{(6t - 3)/t} &> (0.2^{3})^{(2t - 1)/3} \\ 0.2^{(6t - 3)/t} &> 0.2^{3 \cdot [(2t - 1)/3]} \\ \frac{6t - 3}{t} &> 3 \cdot \frac{2t - 1}{3} \\ t \cdot \frac{6t - 3}{t} &> (2t - 1) \cdot t \\ 6t - 3 &> 2t^2 - t \\ -2t^{2} + 7t - 3 &> 0 \\ 2t^2 - 7t + 3 &< 0 \\ (2t - 1)(t - 3) &< 0 \\ \end{align*} When \(t < \frac{1}{2}\) or \(t > 3\), the product of the factored terms is positive, so the inequality doesn't hold.\\ When \(\frac{1}{2} < t < 3\), the product of the factored terms is negative, so the inequality holds.\\ Substituting the original value of \(t\), we have that \begin{equation*} \boxed{\frac{1}{2} < \ln{x} < 3} \end{equation*} %(3) \begin{align*} 3^{\ln{x} + \ln{x^0} + \ln{x^0} + \cdots + \ln{x^0}} &= 27x^{30} \\ 3^{\ln{x} + \ln{1} + \ln{1} + \cdots + \ln{1}} &= 27x^{30} \\ 3^{\ln{x} + 0 + 0 + \cdots + 0} &= 27x^{30} \\ 3^{\ln{x}} &= 27x^{30} \\ \log_3{3^{\ln{x}}} &= \log_3{27x^{30}} \\ \ln{x} &= \log_3{3^{3}} + \log_3{x^{30}} \\ \ln{x} &= 3 + \log_3{x^{30}} \\ \ln{x} &= 3 + \log_3{x^{30}} \\ \ln{x} &= 3 + \frac{\ln{x^{30}}}{\ln{3}} \\ \ln{x} &= 3 + \frac{30\ln{x}}{\ln{3}} \\ \ln{3} \cdot \ln{x} &= 3\ln{3} + 30\ln{x} \\ 0 &= 3\ln{3} + 30\ln{x} - \ln{3} \cdot \ln{x} \\ (30 - \ln{3})\ln{x} &= -3\ln{3} \\ \ln{x} &= \frac{-3\ln{3}}{30 - \ln{3}}\\ e^{\ln{x}} &= e^{\frac{-3\ln{3}}{30 - \ln{3}}}\\ \Aboxed{x &= e^{\frac{-3\ln{3}}{30 - \ln{3}}}} \end{align*} \end{document}Thank you. Since I have MS word, I sort-of make-do with it’s equation editor,
Been interested in LaTeX for a while, so thanks for this.
No problem! I think it’s definitely worth learning the basics, which I don’t think are too bad, and are really plenty unless you have very specific needs or want to make complex diagrams. And regardless, the wizards on StackOverflow are always there to help.
By the way, I just noticed that there’s an issue with the markup I posted due to a known Lemmy bug where ^ gets replaced with the
supHTML tag even in code blocks. I’ll post a proper Pastebin or something when I get the chance!I thought that the LaTeX code used a syntax similar to html.
Thanks a lot.
No problem! Yeah, as you can see it’s a bit different–basically, you’ve got commands that start with backslashes, which can have one or more arguments contained in curly brackets. The most important thing to understand is probably math mode which is what enables all the fancy mathematical typesetting.
Here’s the Pastebin with the correct markup for my earlier comment:
For problem two: I got to the answer by substituting a = 0.2^3 if you try that, you’ll get two roots with the same things inside, leading you to compare only the root exponents
For problem 3: you’re on the right track, just change the base of the logarithm on the left hand side by remembering ln(x) =log 3 (x)/log 3(e). From there, you just need to isolate all the x on one side, the log 3(e) on the other, and do 3 to the power of that to get just x on the left-hand side. Then you can use that property of logarithms on the right hand side to get all the log 3(e) in terms of ln(3) and simplify some more.
Thanks heaps—managed to get them both! It’s good to know I wasn’t too far off. I had a feeling I needed to do change of base but I wasn’t exactly sure where I needed to go with it.
-
i guess these would be difficult back when most people haven’t finished primary school, but these are just basic high school math problems. you just need to know properties of logarithm and a little bit of trigonometry.
In a way, true.
How is the education system in your country?
In my country India, sin, cos, tan, log etc. are introduced in high school, 8th or 9thstandard.
Though, the knowledge with the identities that’d be needed to solve the problems would be taught for those who chose the Science stream for the 11th and 12th standard(We call it Higher Secondary, students would be 16 - 17 years old).So, most people who took +2 Science would be able to solve this.
https://en.wikipedia.org/wiki/Education_in_India#Structure_of_school_education
I asked the question because I wanted to know if high school means the same as we have it here, in India.
im in iran and our education system is piss wrapped inside shit. we learn these in 10th and 11th grade (15 - 17 yo) for science and math students, and basically you should be able to solve each of these under 45 seconds for your university entrance exam (although it’s multiple choice so a little bit easier than full explanation).
i doubt most people would be able to solve these after high school because the stress of the university entrance exam will make sure your brain forgets all this stuff as a protection mechanism to prevent PTSD flashbacks.
So our countries are similar in that aspect, I guess.
I actually like this. I’m not a very fast test taker. I like to see derivations n all and the step-by-step process of solving.
I was lucky with a really good teacher teaching the basics during highschool.
im in iran and our education system is piss wrapped inside shit.
lol from your description it’s still better than in the west
im sorry but it’s really not. it’s miserable as hell.
Why is that? What is it like?
well aside from shitty teachers, under funding and crowded class rooms, lack of any extracurricular activity besides maybe playing football on asphalt and the mostly failed but constant attempts at indoctrination, at best it’s like the Gaokao situation in china, where all your childhood is spent for studying for this massive hard exam at the end, and the society including your parents (if you have any) are constantly drilling it into your head that you would be nothing if you don’t get into a good university. it’s a marathon of pressure and mental abuse from every corner. people either give in, lash out or outright break.
and nobody does anything about it because of capitalism. education is now a very profitable industry. everyone knows that the education system is fucked but any attempt at reform is met with resistance from publishers fearing losing book sales and tutor and private exam companies losing sales (we call them “Konkour mafia”, Konkour is the name of our university entrance exam).
Thanks for the insight comrade. Sounds indeed an order of magnitude shittier than my western education.
I feel like if I actually went through the Soviet education system I might be able to do this but my capitalist education was so lacking that I wouldn’t even know where to start
One of my math professors grew up in soviet Romania and sometimes told us about what math they were taught when.
He said they were taught some relatively high up stuff (by American math standards) in high school. Some reasonably serious group theory apparentlyTo the factory floor with you.
I went to engineering school and some of those I have no idea how to solve. I might be rusty though, I haven’t done any serious math in over 10 years.
ETA: i had just woken up and groggy. They’re not actually all that bad, I might give them a try later today.
If you get the chance I would actually like to know the answer genuinely.
Fake. All soviets did were live in huts, shoot 17th century rifles, and failed basic economics
All Soviets did was eat hot bread and lie
Didn’t they drink vodka?
I have a natural understanding of angles and momentum, but I also got some dyscalcula going on
Would probably make a decent marksman even though my heart wants to make lots of fire
I have a natural understanding of angles and momentum, but I also got some dyscalcula going on
You’ll represent the USSR at the snooker world championship.
In all seriousness, the best billiards players I’ve played with were either: physics PhD candidates or people who couldn’t for the life of them do any math, but just got the game. Both were very fun to lose to.



















